1023. Continued fractions
Let b0, b1,
b2, ..., bn be integers with bk > 0 for k > 0. The continued fraction of order n with coefficients b1,
b2, ..., bn and the
initial term b0 is defined
by the following expression
which can be abbreviated as [b0;
b1, ..., bn].
An example of a continued fraction of order
n = 3 is [2; 3, 1, 4]. This is equivalent to
Write a program that determines the
expansion of a given rational number as a continued fraction. To ensure
uniqueness, make bn > 1.
Input. Consists
of an undetermined number of rational numbers. Each rational number is defined
by two integers, numerator and denominator.
Output. For
each rational number output the corresponding continued fraction on a separate
line.
|
Sample
input |
Sample
output |
|
43 19 1 2 |
[2;3,1,4] [0;2] |
SOLUTION
continued fractions
Algorithm analysis
The fraction a / b
can be written in the next form:
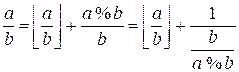
To expand the
rational number a / b into a continued fraction, you should
write its integer part 
, and then, in the presence of a fractional part, you should
expand the number b / (a % b)
into a continued fraction.
Example
= 
= 
= 
= 
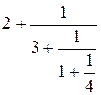
Thus 43 / 19 = [2; 3, 1, 4].
Algorithm realization
We’ll construct a
continued fraction in the array res.
vector<int>
res;
Read the fraction a / b.
while(scanf ("%d
%d",&a,&b) == 2)
{
res.clear();
Convert the fraction to a continued one.
while(b != 1)
{
res.push_back(a/b);
a = a % b;
swap(a,b);
}
res.push_back(a);
Print the continued fraction that corresponds to a / b.
printf("[%d;%d",res[0],res[1]);
for(i = 2; i
< res.size(); i++)
printf(",%d",res[i]);
printf("]\n");
}